Chứng minh trung điểm: Hướng dẫn từng bước, kèm ví dụ dễ hiểu

Trong hình học, khái niệm trung điểm rất quan trọng. Bạn có bao giờ tự hỏi trung điểm của đoạn thẳng là gì? Đặc biệt, các bài tập chứng minh trung điểm thường xuất hiện ở lớp 7. Hãy cùng Cmath tìm hiểu chi tiết qua bài viết này

Trung điểm là gì?

Trung điểm của đoạn thẳng là điểm đặc biệt nằm ngay giữa đoạn thẳng đó, chia đoạn thẳng thành hai phần hoàn toàn bằng nhau. Điểm này không chỉ đóng vai trò quan trọng trong hình học phẳng mà còn là nền tảng cho nhiều khái niệm toán học phức tạp hơn.

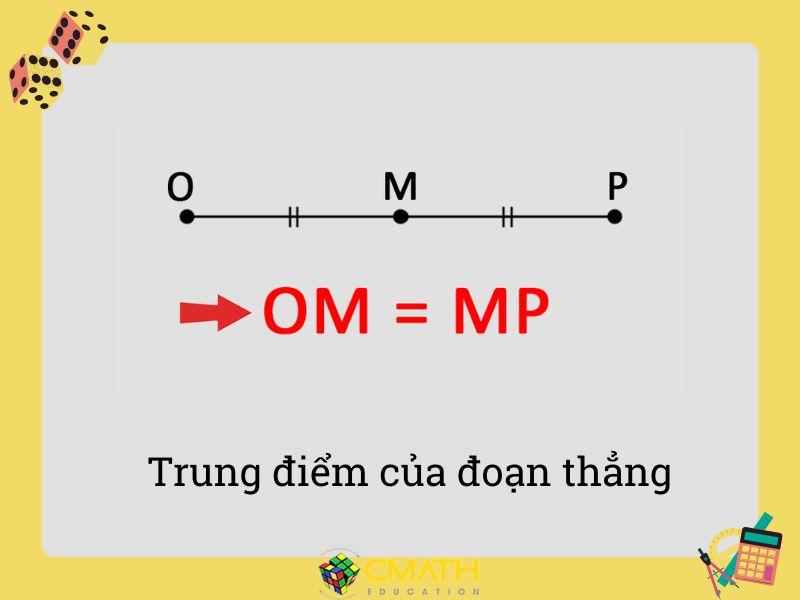
Các yếu tố cốt lõi của trung điểm

Để hiểu rõ hơn về trung điểm, hãy cùng điểm qua các yếu tố quan trọng:

• Đoạn thẳng: Là một phần của đường thẳng, giới hạn bởi hai điểm đầu mút.
• Nằm giữa: Điểm trung điểm phải nằm trên đoạn thẳng, không trùng với hai đầu mút.
• Chia đôi: Khoảng cách từ trung điểm đến mỗi đầu mút phải bằng nhau.

Công thức tính trung điểm và các tính chất của trung điểm

Các tính chất trung điểm của đoạn thẳng:

• Mỗi đoạn thẳng chỉ có một trung điểm Một đoạn thẳng chỉ có thể có duy nhất một trung điểm. Điều này đảm bảo tính chính xác và duy nhất trong các bài toán hình học.

Hướng dẫn chi tiết cách vẽ trung điểm

Bạn muốn tự tay vẽ trung điểm một cách chính xác? Hãy làm theo các bước sau:

Vẽ bằng compa

Compa là trợ thủ đắc lực giúp bạn vẽ trung điểm một cách hoàn hảo:

• Bước 1: Vẽ đoạn thẳng AB.
• Bước 2: Mở compa với bán kính lớn hơn một nửa độ dài AB.
• Bước 3: Vẽ hai đường tròn: một tâm A, một tâm B.
• Bước 4: Hai đường tròn cắt nhau tại C và D. Nối C và D.
• Bước 5: Đường thẳng CD cắt AB tại M. M chính là trung điểm!

Vẽ bằng thước

Nếu không có compa, bạn vẫn có thể vẽ trung điểm bằng thước:

• Bước 1: Đo độ dài đoạn thẳng AB bằng thước.
• Bước 2: Chia đôi số đo vừa tìm được.
• Bước 3: Đặt thước lên đoạn thẳng AB, đánh dấu điểm M sao cho AM bằng một nửa độ dài AB.

Gấp giấy tìm trung điểm

Đây là một cách tiếp cận thú vị và trực quan:

• Bước 1: Vẽ đoạn thẳng AB trên giấy.
• Bước 2: Gấp giấy sao cho A trùng với B.
• Bước 3: Nếp gấp chính là đường thẳng đi qua trung điểm M của AB!

Bật mí cách tính trung điểm đơn giản

Chứng minh một điểm là trung điểm, nghe có vẻ khó, nhưng thực chất lại rất đơn giản nếu bạn nắm vững các phương pháp sau:

Cách 1: Dựa vào tính chất của trung điểm

Để chứng minh một điểm là trung điểm của một đoạn thẳng, chúng ta cần dựa vào định nghĩa của trung điểm. Giả sử chúng ta có ba điểm A, B và C. Chúng ta muốn chứng minh rằng điểm B là trung điểm của đoạn thẳng AC.

• Bước 1: Chứng minh rằng điểm B nằm trên đoạn thẳng AC và nằm giữa hai điểm A và C. Điều này có nghĩa là ba điểm A, B, C phải thẳng hàng và theo đúng thứ tự đó.
• Bước 2: Chứng minh rằng điểm B chia đoạn thẳng AC thành hai đoạn thẳng bằng nhau. Tức là, độ dài của đoạn thẳng AB phải bằng độ dài của đoạn thẳng BC (AB = BC). Đồng thời, tổng độ dài của hai đoạn thẳng AB và BC phải bằng độ dài của đoạn thẳng AC (AB + BC = AC).

Nếu chúng ta chứng minh được cả hai bước trên, chúng ta có thể kết luận rằng điểm B chính là trung điểm của đoạn thẳng AC. Điều này có nghĩa là B thỏa mãn tất cả các điều kiện cần thiết: nằm trên đoạn thẳng AC, chia đoạn thẳng AC thành hai phần bằng nhau, và tổng độ dài hai phần đó bằng độ dài đoạn thẳng AC.”

Cách 2: Chứng minh dựa vào các tính chất của tam giác

Để chứng minh các bài toán liên quan đến trung điểm trong tam giác, bạn cần nắm vững một số tính chất quan trọng. Hãy cùng tìm hiểu về những tính chất này trong tam giác ABC, với M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB:

Đường trung tuyến:

• Các đường thẳng AM, BN, CP được gọi là các đường trung tuyến của tam giác ABC. Đường trung tuyến là đường thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện.

Trọng tâm:

• Ba đường trung tuyến AM, BN, CP luôn cắt nhau tại một điểm duy nhất, điểm này được gọi là trọng tâm của tam giác, ký hiệu là G.
• Trọng tâm G chia mỗi đường trung tuyến thành hai đoạn, trong đó đoạn từ đỉnh đến trọng tâm dài gấp đôi đoạn từ trọng tâm đến trung điểm cạnh 1 đối diện. Cụ thể: AG/AM = BG/BN = CG/CP = 2/3

Đường trung bình:

• Đường thẳng MN, nối trung điểm M và N của hai cạnh BC và CA, được gọi là đường trung bình của tam giác ABC.
• Đường trung bình MN luôn song song với cạnh còn lại của tam giác, tức là song song với cạnh AB (MN // AB).
• Độ dài của đường trung bình MN bằng một nửa độ dài của cạnh song song với nó, tức là MN/AB = 1/2.

Cách 3: Chứng minh dựa vào tính chất tứ giác đặc biệt

Một cách để chứng minh trung điểm là sử dụng các hình tứ giác đặc biệt như hình thang cân, hình bình hành, hoặc hình chữ nhật. Những hình này có tính chất là đường chéo của chúng cắt nhau tại trung điểm của mỗi đường. Ví dụ, trong một hình bình hành, điểm giao nhau của hai đường chéo chính là trung điểm của cả hai đường chéo đó.

Trong hình thang ABCD với hai đáy AB và CD, đường trung bình MN được định nghĩa như sau: MN phải song song với hai đáy (MN // AB và MN // CD), và độ dài của MN bằng trung bình cộng của độ dài hai đáy. Cụ thể, MN = 1/2 (AB + CD). Ở đây, M và N lần lượt là trung điểm của hai cạnh bên AD và BC.

Cách 4: Chứng minh trung điểm dựa vào tính chất của đường tròn

Trong hình học đường tròn, có một định lý quan trọng giúp chứng minh trung điểm. Định lý này nói rằng: trong một đường tròn có tâm O và đường kính AB, nếu đường kính AB vuông góc với một dây cung MN, thì AB sẽ đi qua trung điểm của MN. Ngược lại, nếu AB đi qua trung điểm của MN, thì AB sẽ vuông góc với MN. Định lý này rất hữu ích khi làm việc với các bài toán liên quan đến đường tròn, giúp ta xác định vị trí của các điểm và đoạn thẳng.

Cách 5: Chứng minh trung điểm dựa vào tính chất đối xứng

Tính chất đối xứng cũng là một công cụ mạnh mẽ để chứng minh trung điểm. Hai điểm A và B được gọi là đối xứng nhau qua một đường thẳng d nếu thỏa mãn hai điều kiện:

• Đường thẳng d là đường trung trực của đoạn thẳng AB. Điều này có nghĩa là d vuông góc với AB tại một điểm M, và điểm M này chính là trung điểm của AB.
• Khoảng cách từ điểm A đến đường thẳng d bằng khoảng cách từ điểm B đến đường thẳng d.

Ghi nhớ nằm lòng để chinh phục mọi bài toán về trung điểm

• Luôn nhớ định nghĩa và tính chất của trung điểm.
• Luyện tập vẽ trung điểm bằng nhiều phương pháp khác nhau để tăng kỹ năng.
• Vận dụng linh hoạt các phương pháp chứng minh trung điểm.
• Không ngại thử sức với các bài toán khó để nâng cao trình độ.

Trung điểm đoạn thẳng không chỉ là một khái niệm hình học đơn thuần, mà còn là một người bạn đồng hành quan trọng trong suốt quá trình học tập và khám phá thế giới toán học của bạn. Hãy nắm vững kiến thức về trung điểm và áp dụng chúng một cách linh hoạt để đạt được điểm cao nhé!

Bí quyết chinh phục môn toán: Cmath đồng hành cùng bạn!

Bạn muốn bứt phá trong môn Toán và đạt điểm cao trong các kỳ thi? Hãy đến với Cmath - Trung tâm bồi dưỡng Toán hàng đầu, nơi khơi dậy niềm yêu thích Toán học và phát triển tư duy logic cho học sinh mọi cấp độ. Với đội ngũ giáo viên giàu kinh nghiệm, phương pháp giảng dạy hiện đại và môi trường học tập thân thiện, Cmath cam kết giúp bạn đạt được thành công trong môn Toán!

>>> Xem ngay: Danh sách các khóa học của Cmath